
Solved Recall The Following Logarithmic Properties 1 Loga X R Loga X 2 Loga X Y Loga X Loga Loga X Loga Y Example 1 Expand Each Logarithm Using The
taking the square root of both sides we get LATEXR=\pm (x^2y^2)^\frac {1} {2} /LATEX and taking that up to the third power we get LATEXR^3=\pm (x^2y^2)^\frac {3} {2} /LATEX so that whole right side is equal to LATEXR^3 /LATEX Last editedThe second term of the sum is equal to Y The second factor of the product is equal to a sum consisting of 2 terms The first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plus negative Y close parenthesis;
Expand (1/x+y/3)^2
Expand (1/x+y/3)^2-Simplify (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each termREMARK The greatest coefficient in the expansion of (x 1 x 2 x m) n is (n!) / (q!) m – r {(q1)!} r, where q and r are the quotient and remainder, respectively when n is divided by m Multinomial Expansions Consider the expansion of (x y z) 10 In the expansion, each term has different powers of x, y, and z and the sum of
What Is The Binomial Expansion For 1 X 1 Quora
Y2 ⋯ Πk j=1(n j − 1) k!How Do You Expand \( (1x)^3 \)?Expand and simplify polynomials This calculator will try to simplify a polynomial as much as possible It works with polynomials with more than one variable as well The calculator will show you all steps and easytounderstand explanations on how to simplify polynomials
The function you want to Taylor expand is y(x)=(1x)^n Then your Taylor expansion is y(x)=y(0)y'(0)xy''(0)x^2/2!Expand (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Multiply by Add and Eg x*x^(n2)*y cancels y*x^(n1), x*x^(n3)*y^2 cancels y*x^(n2)*y I know you can't write out all of the terms You'll have to use the '' to express what you mean
Expand (1/x+y/3)^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
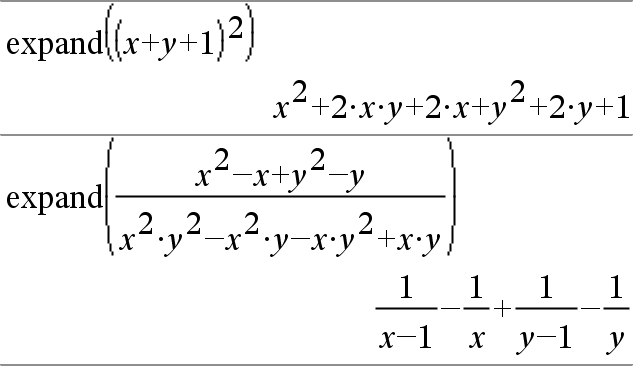 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
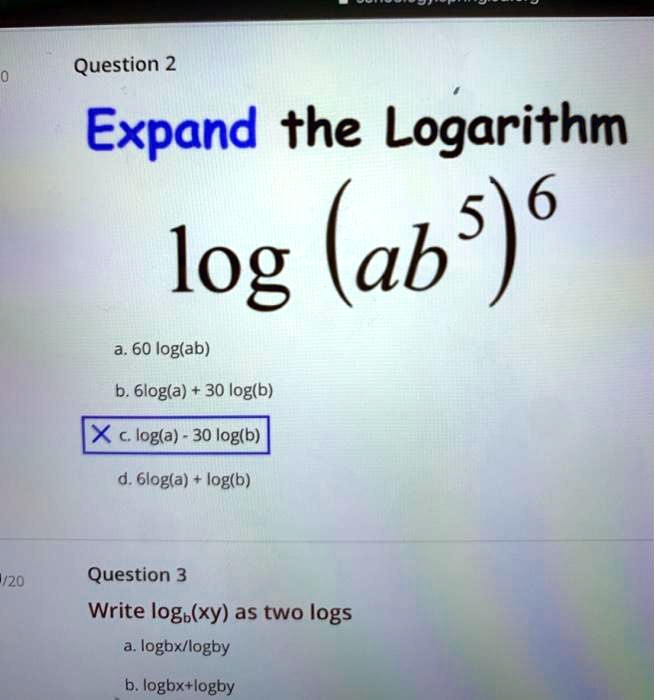 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
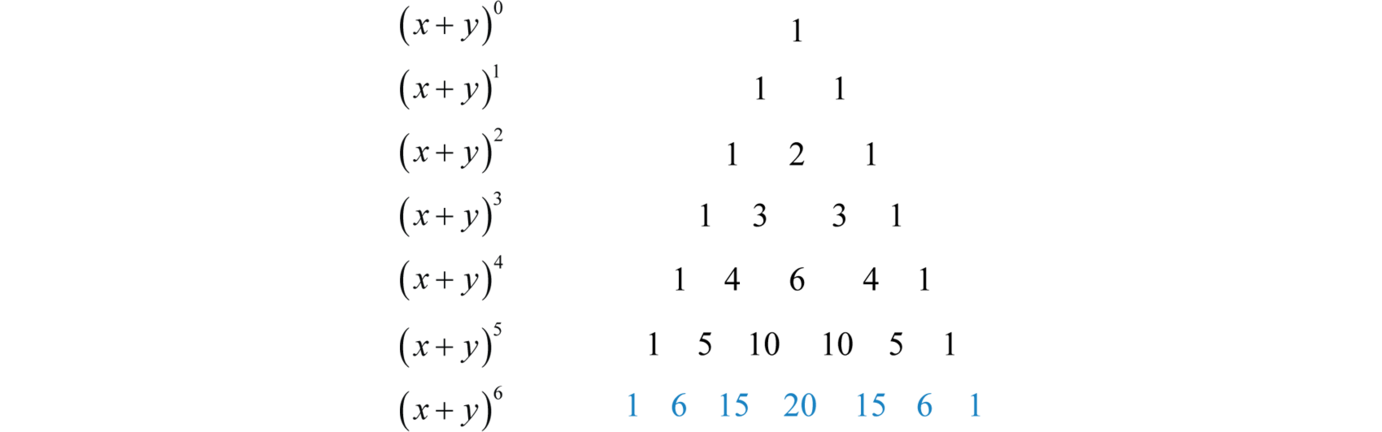 Wolfram Alpha Examples Step By Step Solutions | 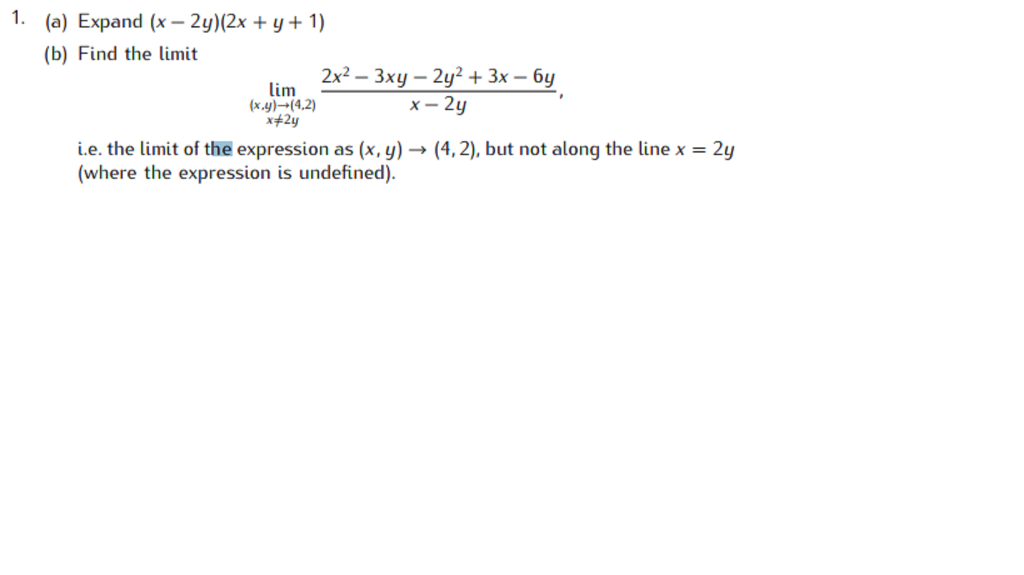 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
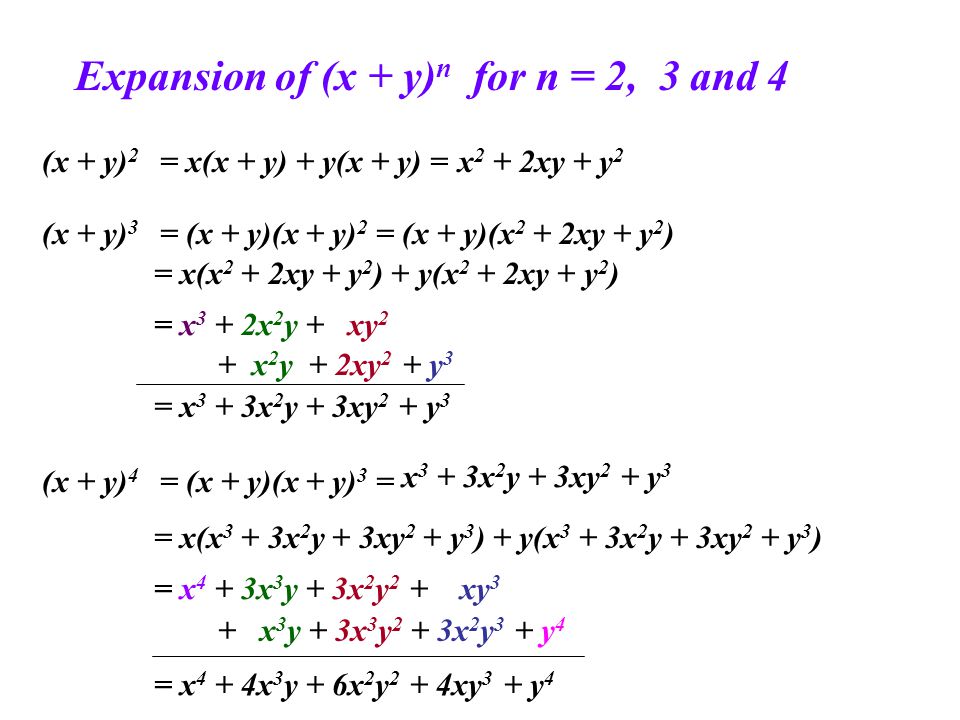 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | 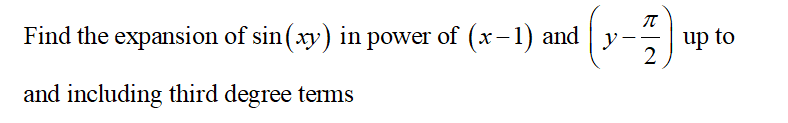 Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | 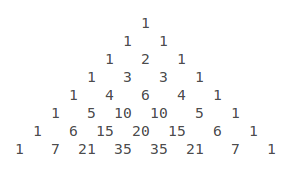 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions | 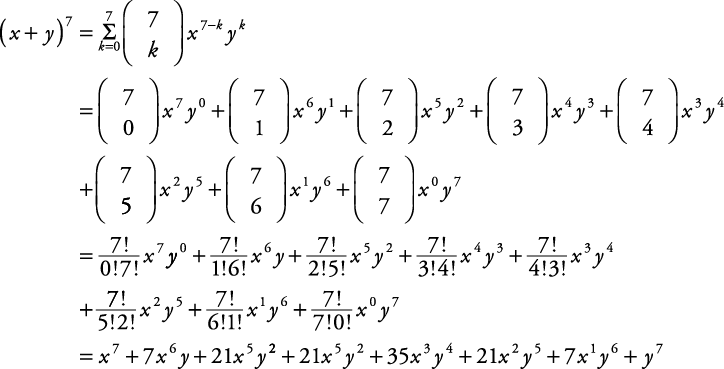 Wolfram Alpha Examples Step By Step Solutions |
Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
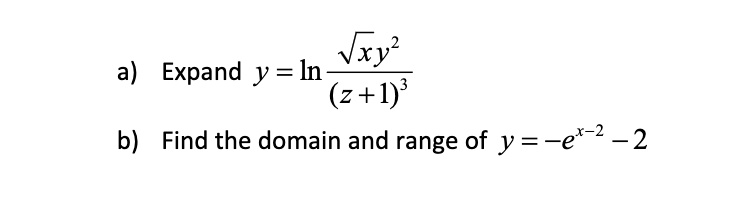 Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |  Wolfram Alpha Examples Step By Step Solutions |
 Wolfram Alpha Examples Step By Step Solutions | Wolfram Alpha Examples Step By Step Solutions |
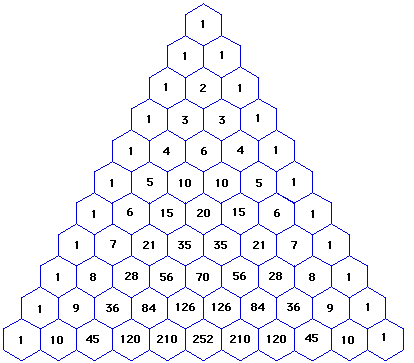
The calculator allows you to expand and collapse an expression online , to achieve this, the calculator combines the functions collapse and expand For example it is possible to expand and reduce the expression following ( 3 x 1) ( 2 x 4), The calculator will returns the expression in two forms expanded and reduced expression 4 14 ⋅ xThe exponents of x descend, starting with n, and the exponents of y ascend, starting with 0, so the r th term of the expansion of (x y) 2 contains x n(r1) y r1 This information can be summarized by the Binomial Theorem For any positive integer n, the expansion of
Incoming Term: (1-x-y)^2 expand, expand (1/x+y/3)^2,




0 件のコメント:
コメントを投稿