最高のコレクション (1-x-y)^2 expand 266103

Plos Genetics A Tandem Duplicate Of Anti Mullerian Hormone With A Missense Snp On The Y Chromosome Is Essential For Male Sex Determination In Nile Tilapia Oreochromis Niloticus

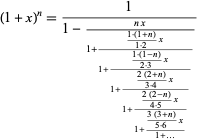
BINOMIAL THEOREM 133 Solution Putting 1 2 − =x y, we get The given expression = (x2 – y)4 (x2 y)4 =2 x8 4C2 x4 y2 4C 4 y4 = 2 8 4 3 4 2(1– ) (1 )2 2 2 1 × ⋅ − × x x x x = 2 x8 6x4 (1 – x2) (1 – 2x2 x4=2x8 – 12x6 14x4 – 4x2 2 Example 5 Find the coefficient of x11 in the expansion of 12 3 2 2 − x x Solution thLet the general term, ie, (r 1A =1 Solution (a) We shall use (1) by &rst rewriting the function as follows 1 1x2 1 1¡(¡x2) y==¡x2 1 1¡y = X1 n=0 yn;

(1-x-y)^2 expand

(1-x-y)^2 expand-2 Expand and simplify with two or more brackets Expand the brackets to give the following expression Eg (x 5)(x − 1) = x 2 5x − x − 5 = x 2 4x − 5 Remember expressions with three terms like x 2 4x − 5 are known as trinomials An expression that contains more than two terms and includes variables and coefficients is Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Plos One Sensitivity Analysis For Reproducible Candidate Values Of Model Parameters In Signaling Hub Model

(c) h(x)= 1 2x3;So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) Generally It is, of course, often impractical to write out Pascal"s triangle every time, when all that we need to know are the entries on the nth line Expand the following `(i) (3a2b)^(3) (ii) ((1)/(x)(y)/(3))^(3)` (iii) `(4(1)/(3x))^(2)`

1 Expand the brackets by multiplying (2 x 3) by x and (2 x 3) by −5 2 Simplify by collecting like terms 3x − 10x = −7x Practice 1 Expand a 3(2x 2− 1) b −2(5pq 4q) c −(3 xy − 2 y 2) 2 Expand and simplify a 7(3 x 5) 6(2 x – 8) b 8(5 p – 2) – 3(4 p 9) c 9(3 s 1) –5(6 s – 10) d 2The first factor of the product is a sum containing 2 terms The first term of the sum is equal to X The second term of the sum is equal to Y The second factor of the product is equal to a sum consisting of 2 terms The first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plusSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

(1-x-y)^2 expandのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	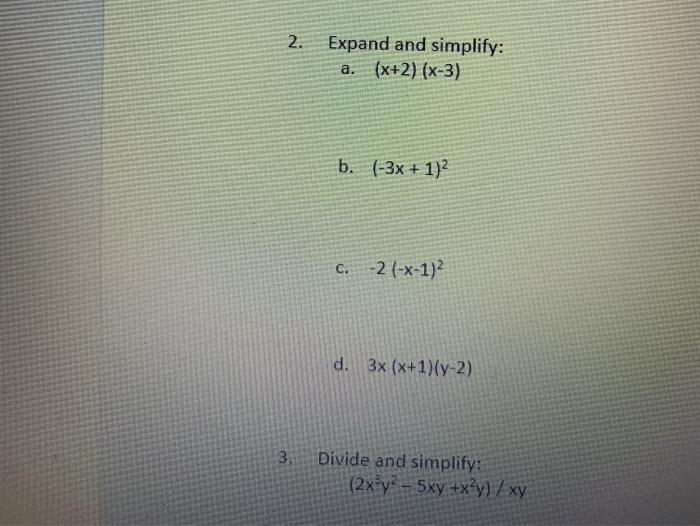Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia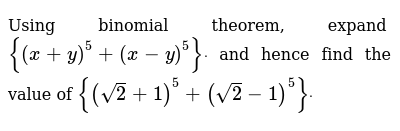
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
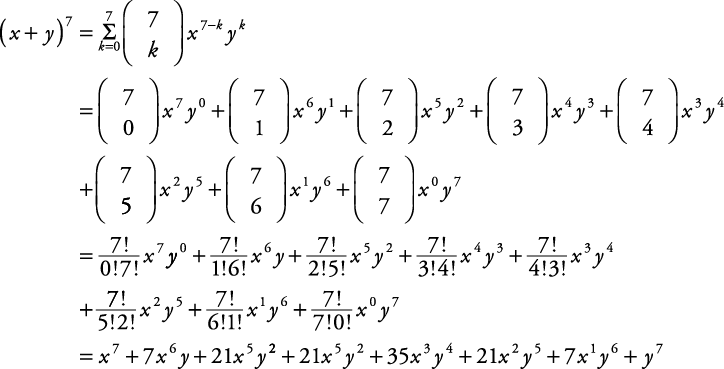Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	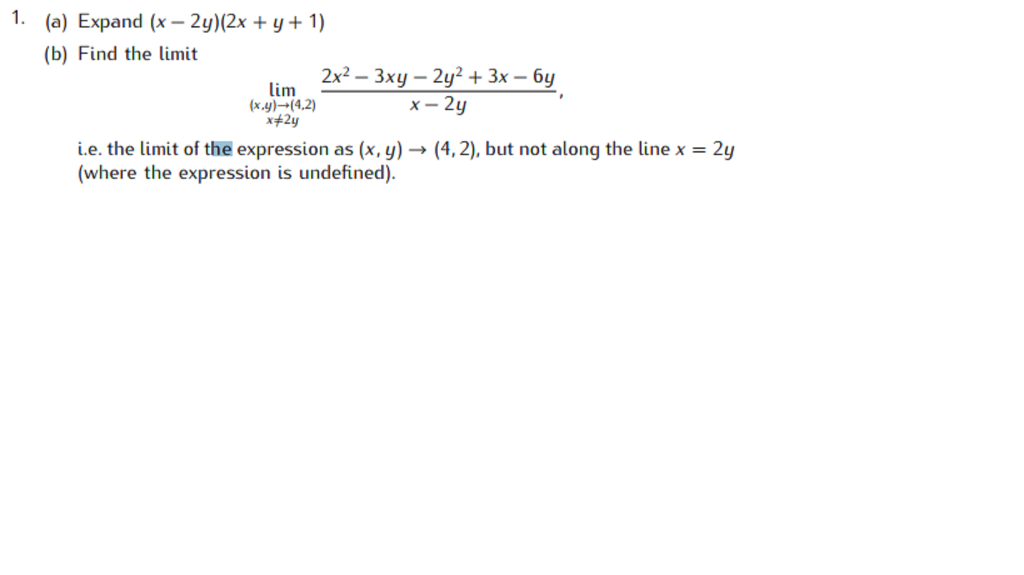Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	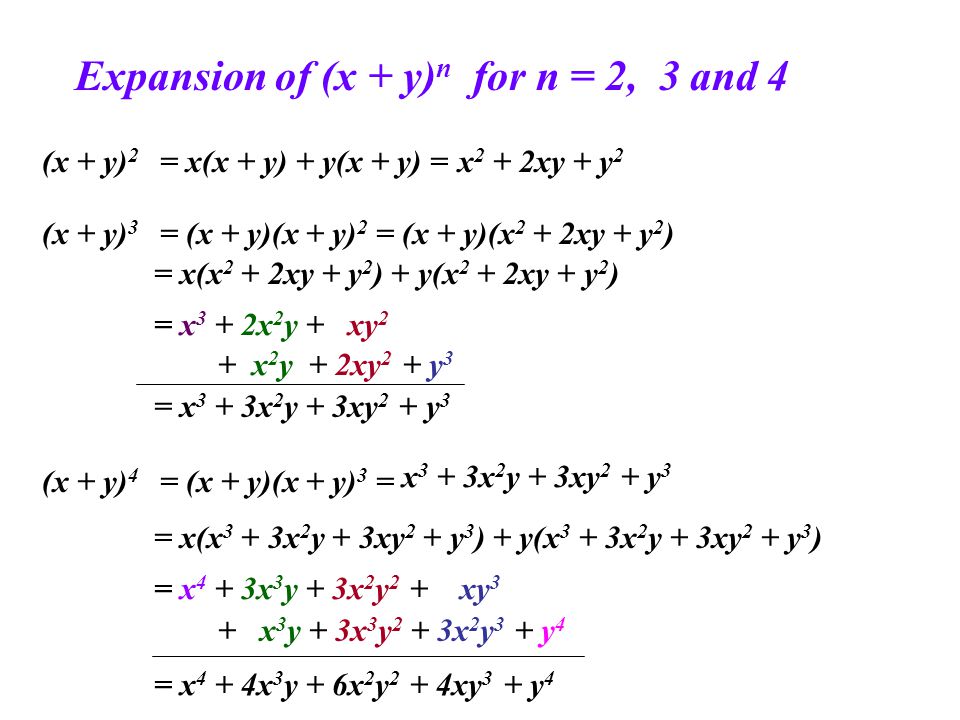Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	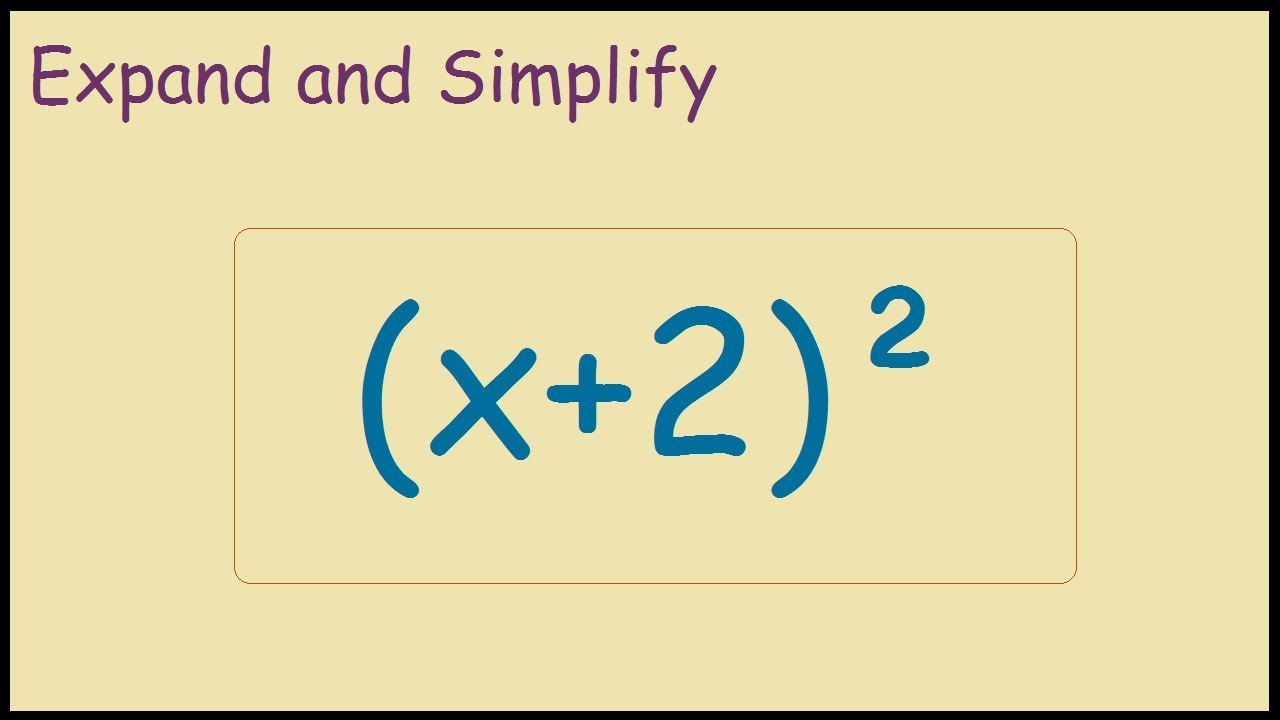Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia	Binomial Theorem Wikipedia
Binomial Theorem Wikipedia	Binomial Theorem Wikipedia

 (b) g(x)= x x2;Expandcalculator expand \left(x1\right)^{2} en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the2 This expansion is for the case where r0=r1 and this is called the interior expansion 1 j~r ~r0j X l=0 rl r0l1 P l(cos ) rAdding both equations , we get (1x)S = 1 x x^2 x^3 The RHS is an sum of an infinite GP with r = x Sum of an infinite GP is given by a/ (1r) (1x)S = 1/ (1x) S = 1/ (1x)^2 Hence the